11. Some mathematical analyses of electric circuit phenomena
11.2 Trapped voltages during bus charging current switchings by disconnectors

Previous

Next

Contents

Disconnectors are switching facilities that can switch only negligibly small currents such as in the order of less than 0.5 A. In electrical stations, the main currents are switched by circuitbreakers, and series connected disconnectors switch only the charging currents of the buses between the circuit-breakers and the disconnectors. Charging current switching phenomena are generally considered in chapter 3. In those general cases, the trapped voltage in the load side capacitances are mostly 1 p.u. because of the steady current interruptions at current zeros, i.e. at voltage peaks. On the other hand in switching very small charging current by a disconnector, the following conditions are introduced.:

• The current can be interrupted at any time irrespective of current zero or not while the contacts are open.
  
• Due to the relatively slow opening speed of the contacts, the separated contact flashovers (re-strike) multiple times depending on the contact's distance and the applied (recovery) voltage.
  
• The re-strike current is of high amplitude and high frequency one, so within very short time interval it is damped and can be re-interrupted.
  
• The trapped (residual) load side voltage is practically equal to the instantaneous source voltage at each interruption and kept until the next re-strike.
  
• For certain disconnectors, re-striking (discharging) voltage asymmetry appear ----- different discharging voltages depending on the polarities of the applied voltages.
  

Fig. 11.2 shows an example of such phenomenon. What is most interesting in it is the trapped voltage is far less than 1 p.u., and the maximum restriking voltage (voltage across the contacts before restriking) is also far less than 2 p.u. on the contrary to what was talked in chapter 3. Therefore the created over-voltages are hoped to be lower than the maximum estimated value.

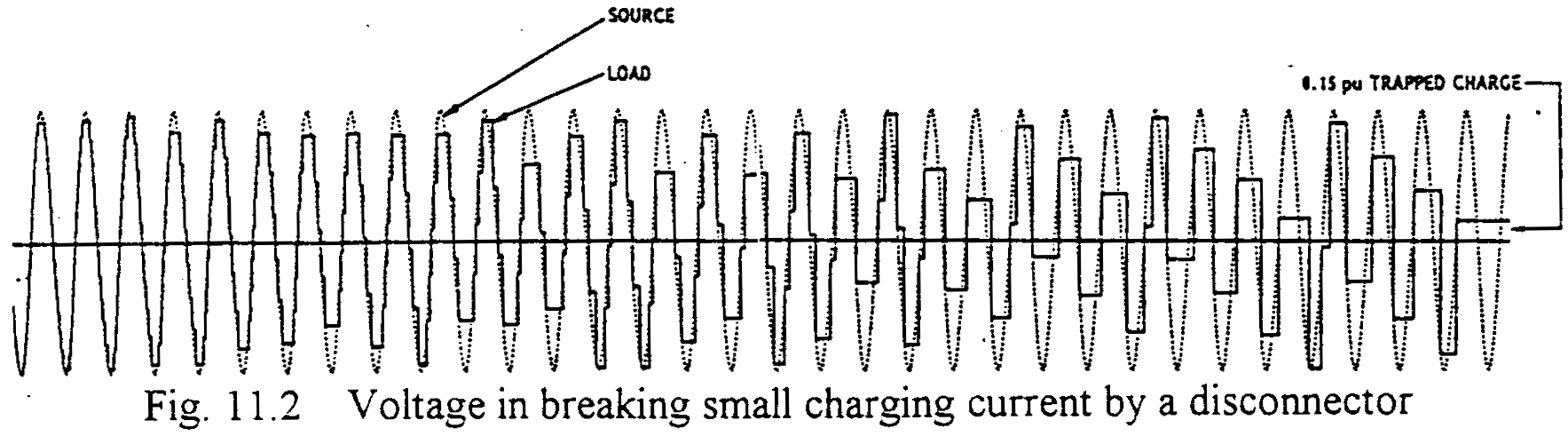
The magnitudes of the re-striking and the created surge voltages are important because of the following two reasons.:

a) Might be creating flash-over faults between the contacts and the grounds (due to the surge voltage applications during hot conditions)
b) Induced surge voltages in low voltage control circuits

The trapped voltages depend on the asymmetry of the discharging voltages between the contacts, velocities of the contact openings and the scatterings of the discharging voltages. Therefore, to calculate the maximum trapped/discharging voltages, statistical mean had been necessitated. To obtain one nomograph of trapped voltage density distribution (see the attached figure in Appendix 11.2), several thousands of simulation calculations had been carried out applying random numbers. For disconnector technology or testing purpose, only the maximum value have been required. For this, much more simplified method had been wished.
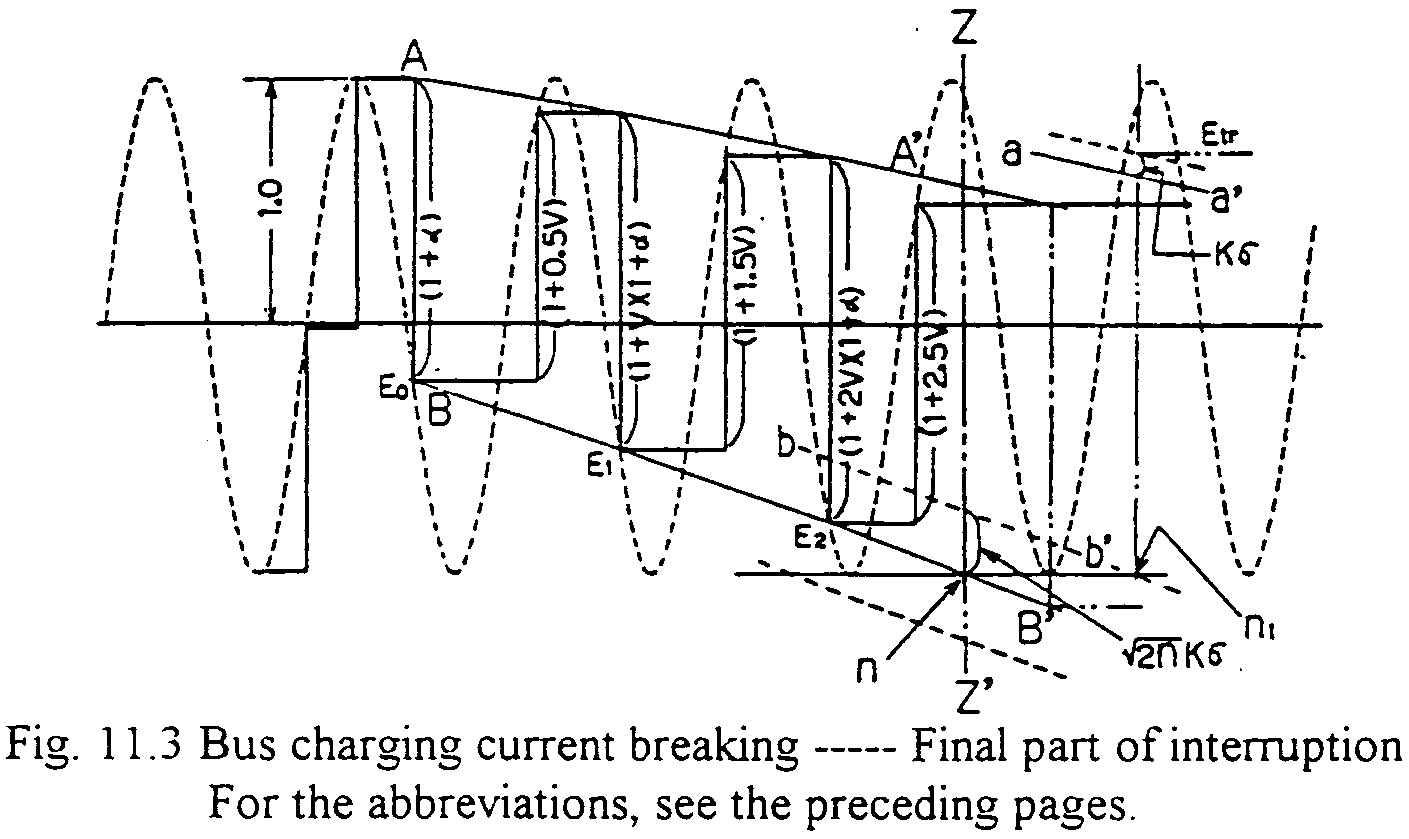
Fig. 11.3 shows the final part of the current interruption in detail. Introducing the abbreviations followed, equations (11)---(15) are obtained. (For details, see the attached literature.)

Assumptions --- Every value is normalized
e_s: Source voltage
e_L: Load side (capacitance) voltage
e₁,e₂: Restriking (discharging) voltages of positive and negative polarities
a: Asymmetry (See equation (11))
V : Contact separation velocity
s: Standard deviation of the restriking voltage scatterings
E_tr: Trapped voltage
n : Number in cycles of source voltage

From the definition,

a=(e₁-e₂)/e₂

In Fig. 11.3, firstly excluding (not considering) the effect by the scattering of the discharging voltages, then,

For a=0
E₀=- a
E₁=E₀+(1+0.5V)-(1+V)(1+a)
=-2a-0.5V-a
En=-(n+1) a-0.5nV-0.5n(n+1)aV ---- (12)

At ZZ', E_n= -1, and assuming that n can be continuous number, then,

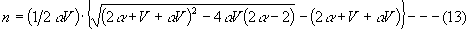
As for the scatterings, it can be said that the scattering of a value consists of n numbers with scatterings of s is square root n times s, then as the effect of the scatterings, n is shifted to n₁ such as,

Finally E_tr is obtained as,

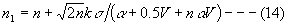
E_tr=a+n₁V+ks --- (15)

Comparing to the results of statistically simulated one which needs more than ten thousands of time to calculate, the results by the simplified methods here mentioned coincides. Generally speaking, statistical handlings need huge amount of calculations, but in certain cases, such analytically geometrical solutions can be a beneficial alternatives of much time losing statistical means.

---

This page is based on Prof. E.Haginomori's lectures in Tokyo Institute of Technology, and edited by Japanese ATP User Group. Copyright (C) Eiichi Haginomori and Japanese ATP User Group.