2. Short-circuit current breaking phenomena
2.4 TRVs in three phase circuits

Previous

Next

Contents

For breaking phenomena in three phase circuits, current injection principle is also applicable and also convenient to understand. For three-phase transient phenomena, symmetrical coordinate method (symmetrical component transformation method) is also applicable. The basic equations are, :

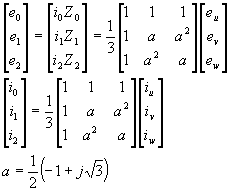
where, Z₀, Z₁, and Z₂ are respective sequence surge impedances seen from the circuit-breaker's relevant terminals, and e₀, e₁ and e₂ are voltages appearing across the terminals of the relevant phase of the circuit-breaker. And for most cases,

Z₁=Z₂

is applicable due to the symmetry of the transmission lines and transformers. For the case of three phase grounding fault current breaking and the phase "u" is the first-phase-to-clear, then, e_v = e_w = 0. From the above shown equations, :

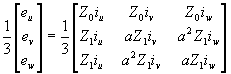
For e_u (voltage across the terminals) and i_u(injecting current), the ratio of which is equal to the equivalent surge impedance,

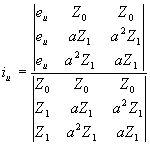
Then for first phase to clear,:

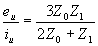
Likewise, for second phase to clear,

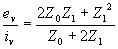
for third phase to clear,

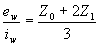
These are the equivalent (surge) impedances seen from the relevant terminals of the circuit-breaker, and the dv/dt's (rate of rise of TRVs) are proportional to the products of these and the fault currents (see Sub-section 1.1).
For actual calculations, EMTP is recommended and mostly convenient, and some examples including cases in the former subsection are attached. Nevertheless, the above shown principles should always be born in mind to check the validity.

---

This page is based on Prof. E.Haginomori's lectures in Tokyo Institute of Technology, and edited by Japanese ATP User Group. Copyright (C) Eiichi Haginomori and Japanese ATP User Group.