The method is called as "R.M.S. value based analysis" For calculations, values corresponding to the respective steady state conditions are considered, i.e., for the torque of the generator which is the most important factor of the phenomena, the steady state values under, such as, no load, loaded, line charging, short-circuited, etc. conditions are considered. (As for transient torque, see the next sub-chapter.) But for another factors such as AVR, PSS, system parameters, damping coefficients, etc., detailed conditions can be introduced and we have had practically enough accurate results. Some program are available and a simple example is shown bellow. (Named "Castle" developed by EPDC.)
Fig. 7.2 shows so called "One machine inf. bus system", where, at t=0.1 sec., a three phase grounding fault occurs in one route of the double circuited transmission line. At t=0.2 sec., the fault is cleared by the circuit-breakers at both ends of the line. Then the power is transmitted
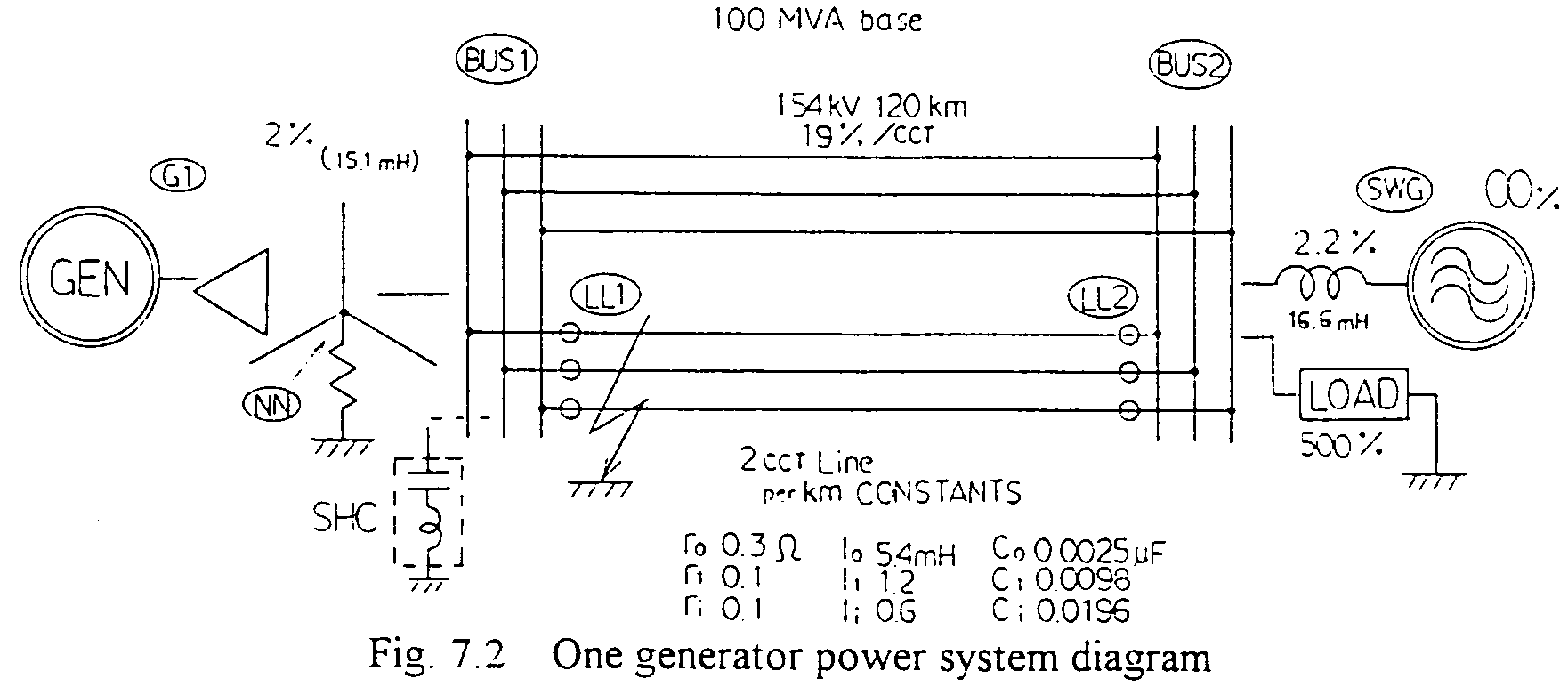
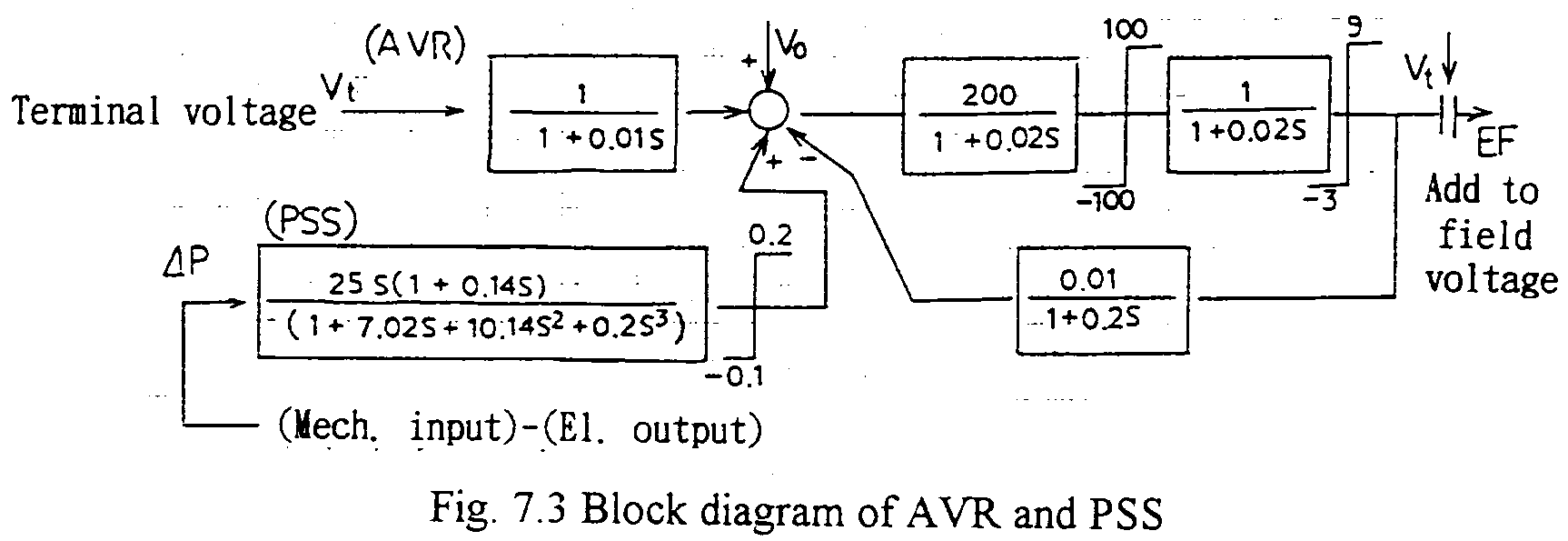
by one route of the line. So the value X in the equation (sub-chapter 7.1) increases. The situation is similar to the second example in the previous sub-clause. But, during short-circuiting, the electrical out put power of the generator is mainly reactive, i.e. the effective power output and related electrical torque is quasi zero. Therefore the mechanical input torque, which is assumed to be constant, is excess, so an area corresponding to the excess energy is to be superimposed to S3 in Fig. 7.1. In the case, high sensitivity effective AVR and PSS are applied to the generator to damp the swing of the angle. The block diagram of the control is shown in Fig. 7.3
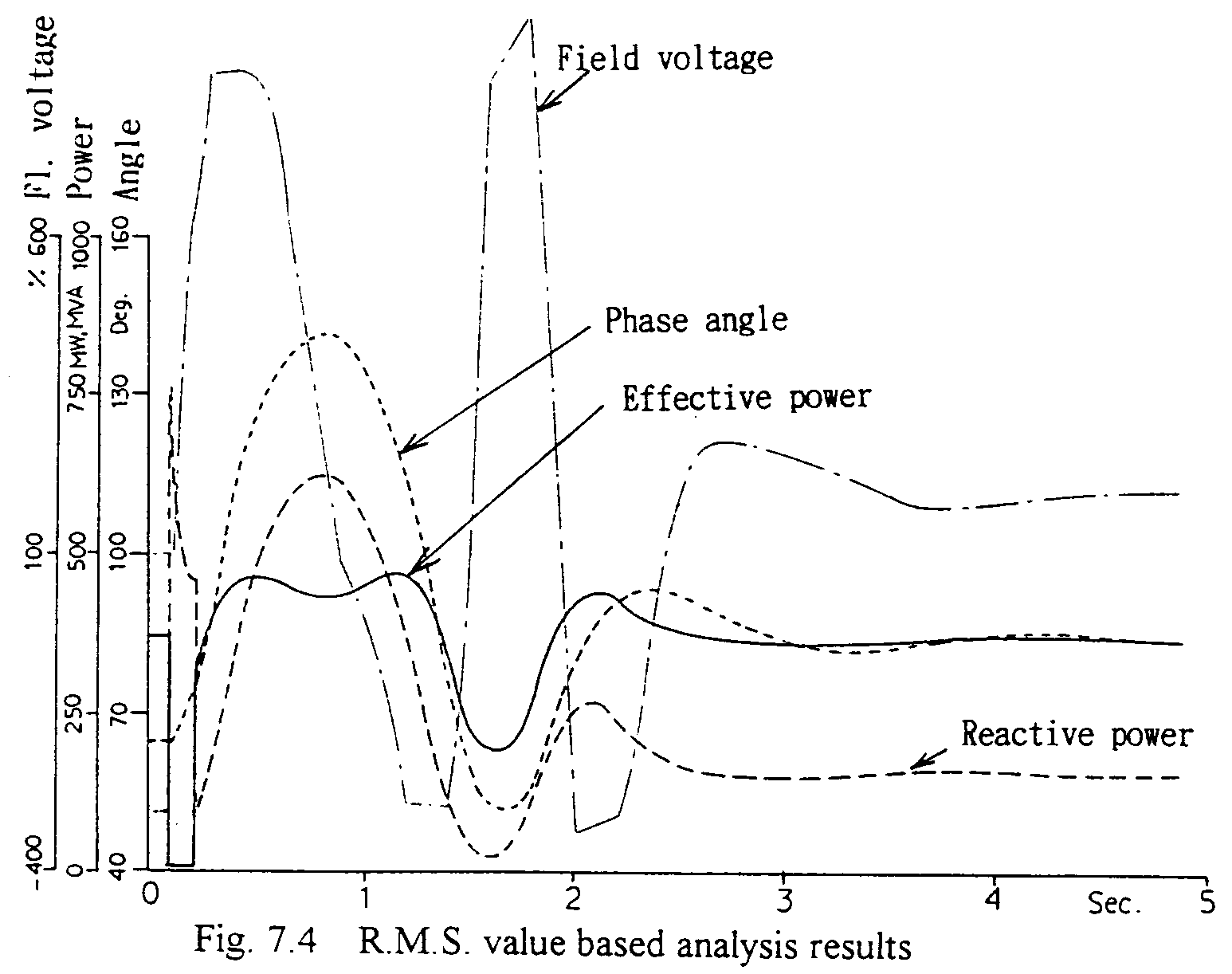
The calculated results are shown in Fig. 7.4. During the short-circuiting interval (0.1s ---0.2s), the generator's effective power output is nearly zero as mentioned before, so due to the excess mechanical torque input, the generator is accelerated. As the result the angle increased. By the self recovery force of the system and the increase of the field excitation by PSS resulting in the increase of the output power, the angle swing is damped, and finally the angle converge to the appropriate value. A lot of such calculations for the actual complicated systems including multi-machines have been carried out to design systems, AVR, PSS, etc.